 |
|
|
МОДЕЛИРОВАНИЕ ИНФОРМАЦИОННЫХ ПРОЦЕССОВ И СИСТЕМ
1. ВВЕДЕНИЕ
Модель — это представление, как правило, в математических терминах наиболее характерных черт изучаемого объекта или системы. Одним из самых распространенных инструментов для математического моделирования и исследования информационных процессов и систем являются Сети Петри. Цель представления системы в виде сети Петри и последующего анализа этой сети состоит в получении важной информации о структуре и динамическом поведении моделируемой системы. Эта информация может использоваться для оценки моделируемой системы и выработки предложений по ее усовершенствованию. Впервые сети Петри предложил немецкий математик Карл Адам Петри [1]. В русскоязычной литературе наиболее полно классические сети Петри представлены в [2] и в [3].
1.1. Природа систем, моделируемых сетями Петри.
Сети Петри предназначены для моделирования систем, которые состоят из множества взаимодействующих друг с другом компонент. При этом компонента сама может быть системой. Действиям различных компонент системы присущ параллелизм. Примерами таких систем могут служить вычислительные системы, в том числе и параллельные, компьютерные сети, программные системы, обеспечивающие их функционирование, а также экономические системы, системы управления дорожным движением, химические системы, и т. д.
1.2. Подходы к проектированию систем с помощью сетей Петри.
В одном из подходов к проектированию и анализу систем сети Петри используются, как вспомогательный инструмент анализа. Здесь для построения системы используются общепринятые методы проектирования. Затем построенная система моделируется сетью Петри, и модель анализируется. Если в ходе анализа в проекте найдены изъяны, то с целью их устранения проект модифицируется. Модифицированный проект затем снова моделируется и анализируется. Этот цикл повторяется до тех пор, пока проводимый анализ не приведет к успеху.
Другой подход предполагает построение проекта сразу в видеĀ сети Петри. Методы анализа применяются только для создания проекта, не содержащего ошибок. Затем сеть Петри преобразуется в реальную рабочую систему.
В первом случае необходима разработка методов моделирования систем сетями Петри, а во втором случае должны быть разработаны методы реализации сетей Петри системами.
2. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
2.1. Теоретико-множественное определение сетей Петри.
Пусть мультимножество это множество, допускающее вхождение нескольких экземпляров одного и того же эллемента.
Определение 2.1. Сеть Петри N является четверкой N=(P,Т,I,O), Āгде
Ę P={p1, p2,...,pn} — конечное множество позиций, n³0;
Ę T={t1, t2,...,tm} — конечное множество переходов, m³0;
Ę I: T « P* — входная функция, сопоставляющая переходуĀ мультимножество его входных позиций;
Ę О: T « P* — выходная функция, сопоставляющая переходу мультимножество его выходных позиций. “
ПозицияĀ pÎP называется входом для перехода tÎT, если pÎI(t). ПозицияĀ pÎP называется выходом для перехода tÎT, если pÎO(t). Структура сети Петри определяется ее позициями, переходами, входной и выходной функциями.
Пример 2.1. Сеть Петри.
N =(P,T,I,O),
P={p1, p2, p3},
T={t1, t2},
I(t1)={ p1, p1, p2},ĀĀĀĀĀĀĀĀĀĀĀĀĀĀ O(t1)={p3},
I(t2)={ p1, p2, p2},ĀĀĀĀĀĀĀĀĀĀĀĀĀĀ O(t12)={p3}.Ā ”
Использование мультимножеств входных и выходных позиций перехода, а не множеств, позволяет позиции быть кратным входом и кратным выходом перехода соответственно. При этом кратность определяется числом экземпляров позиции в соответствующем мультимножестве.Ā
Переход t называется входом для позиции p, если p является выходом для t. Переход t называется входом для позиции p, если p является входом для t. Существуют альтернативные, эквивалентные определения сетей Петри. В частности, функции I и O могут быть определены, таким образом, чтобы сопоставлять позициям входные и выходные мультимножества переходов соответственно.
2.2. Графы сетей Петри.
Наиболее наглядным представлением сети Петри является её графическое представление, которое представляет собойĀ двудольный, ориентированный мультиграф.
Граф сети Петри обладает двумя типами узлов: кружок m, представляющий позицию сети Петри; и планка ¾, представляющая переход сети Петри. Ориентированные дуги этого графа (стрелки) соединяют переход с его входными и выходными позициями. При этом дуги направлены от входных позиций к переходу и от перехода к выходным позициям. Кратным входным и выходным позициям перехода соответствуют кратные входные и выходные дуги.
Пример 2.2. Граф сети Петри определённой в примере 2.1.
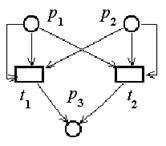 |
”Ā
Определение 2.2. Граф сети Петри есть двудольный, ориентированный мультиграф G=(V,A), где V={v1,v2,...,vk} — множество вершин, а А={a1,a2,...,ar} —мультимножество направленных дуг, и множество V может быть разбито на два непересекающихся подмножества P и T, V=РÈT, PÇT=Æ так, что для любой aiÎA и ai=(vj,vs), (где vj,vsÎv) справедливо либо vjÎP и vsÎT, либо vjÎT и vsÎP.Ā “
Замечание 2.1. ĀСогласно определению графа сети Петри в нём не возможны дуги между двумя позициями и между двумя переходами. “
Замечание 2.2. Теоретико-множественное задание сети Петри N=(P,T,I,O) однозначно определяет граф сети Петри С=(V,A).“
Пример 2.3. Построение графа сети Петри по её теоретико-множественному заданию.
N =(P,T,I,O), P={p1, p2, p3, p4}, T={t1, t2},
I(t1)={ p1, p2},ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ O(t1)={p1, p2,p2,p3,p3},
I(t2)={p2,p3},ĀĀĀĀĀĀĀĀĀĀĀĀ ĀĀĀĀĀĀĀĀO(t2)={ p4,p4,p4}.
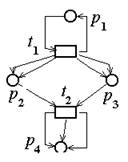 |
”
2.3. Маркировка сетей Петри.
Маркировка — это размещение по позициям сети Петри фишек, изображаемых на графе сети Петри точками. Фишки используются для определения выполнения сети Петри. Количество фишек в позиции при выполнении сети Петри может изменяться от 0 до бесконечности.
Определение 2.3. Маркировка mĀ сети Петри N=(P,T,I,О) есть функция, отображающая множество позиций P в множество неотрицательных целых чисел Nat (где число из Nat обозначает количество фишек, помещаемых в соответствующую позицию). “
Маркировка m, может быть также определена как n-вектор m=<m(p1),m(p2),…,m(pn)> где n=êPê – число позиций в сети Петри и для каждого 1£i£n справедливо m(pi)ÎNat. –количество фишек в позиции pi.
Определение 2.4. Маркированная сеть Петри N=(P,Т,I,О,m) определяется совокупностью структуры сети Петри (P,T,I,О) и маркировки m. “
Пример 2.4. Графического представления маркированной сети Петри.
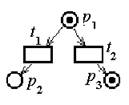 |
m=<1,0,1>. ”
Множество всех маркировок сети Петри бесконечно. Если фишек, помещаемых в позицию слишком много, то удобнее не рисовать фишки в кружке этой позиции, а указывать их количество.
2.4. Правила выполнения сетей Петри.
Сеть Петри выполняется посредством запусков переходов. Запуск перехода управляется фишками в его входных позициях и сопровождается удалением фишек из этих позиций и добавлением новых фишек в его выходные позиции.
Переход может запускаться только в том случае, когда он разрешен. Переход называется разрешенным, если каждая из его входных позиций содержит число фишек, не меньшее, чем число дуг, ведущих из этой позиции в переход (или кратности входной дуги).
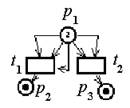 |
Пример 2.5. Разрешённый переход маркированной сети Петри.
В этой сети Петри с маркировкой m=<2,1,1> разрешёнĀ переход t1 и не разрешён переход t2. ”
Пусть функция ^#: P´T«NatĀ для произвольных позицииĀ pÎP и перехода tÎТ задаёт значение ^#(p,t), которое совпадает с кратностью дуги, ведущей из p в t, если такая дуга существует, и с нулём, в противном случае.
Пусть функция #^: T´ P «NatĀ для произвольных и перехода tÎT позицииĀ pÎP задаёт значение #^(t,p), которое совпадает с кратностью дуги, ведущей из t в p, если такая дуга существует, и с нулём, в противном случае.
Пример 2.5. Функции ^# и #^ для сети Петри из примера 2.4.
^#(p1,t1)=3,ĀĀ ^#(p2,t1)=0,ĀĀ ^#(p3,t1)=0,
^#(p1,t2)=2,ĀĀ ^#(p2,t2)=0,ĀĀ ^#(p3,t2)=0,
#^(t1,p1)=0,ĀĀ #^(t1,p2)=1,ĀĀ #^(t1,p3)=0,
#^(t2,p1)=0,ĀĀ #^(t2,p2)=0,ĀĀ #^(t2,p3)=1.Ā ”
Определение 2.5. Переход tÎT в маркированной сети Петри N=(P,T,1,О,m) разрешен, если для всех pÎI(t) справедливо m(p) ³ ^#(p,t).“
Запуск разрешённого перехода tÎT из своей входной позиции pÎI(t)Ā удаляет ^#(p,t) фишек, а в свою выходную позицию p’ÎO(t) добавляет #^(t,p’) фишек.
Пример 2.6. Запуск разрешённого перехода в сети Петри.
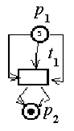 |
Сеть Петри до запуска перехода t1.
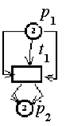 |
Сеть Петри после запуска перехода t1.Ā
”
Запуск перехода заменяет маркировку m сети Петри на новую маркировку m'.
Определение 2.6. Переход t в маркированной сети Петри с маркировкой m может быть запущен всякий раз, когда он разрешен и в результате запуска разрешенного перехода t образуется новая маркировка m', определяемаяĀ следующим соотношением:
m'(p)= m(p) – ^#(p,t) + #^(t,p).
для всехĀ pÎP. “
Пример 2.7. Преобразование маркировки сети Петри в примере 2.6..
Переход t1 преобразует маркировку m=<5,1> в маркировку m’=<2,3>. ”
Запуски могут осуществляться до тех пор, пока существует хотя бы один разрешенный переход. Когда не останется ни одного разрешенного перехода, выполнение прекращается.
Если запуск произвольного перехода t преобразует маркировку m сети Петри в новую маркировку m', то будем говорить, что m' достижима из m посредством запуска перехода t. Это понятие очевидным образом обобщается для случая последовательности запусков разрешённых переходов. Через R(N,m) обозначим множество всех достижимых маркировок из начальной маркировки m в сети Петри N.
3. МОДЕЛИРОВАНИЕ НА ОСНОВЕ СЕТЕЙ ПЕТРИ
В этом разделе рассмотрим ряд примеров моделирования систем сетями Петри, позволяющих дать представление о большом классе систем, которые можно моделировать сетями Петри, об использующемся методе моделирования и о свойствах, которыми должны обладать моделируемые системы. Особое внимание будет уделено системам из областиĀ аппаратного и программного обеспечения и системам управления железнодорожным движением.
3.1. События и условия.
Представление системы сетью Петри основано на двух основополагающих понятиях: событиях и условиях. Возникновением событий управляет состояние системы, которое может быть описано множеством условий. Условие может принимать либо значение ½истина╗, либо значение ½ложь╗.
Возникновение события в системе возможно, если выполняются определённые условия – предусловия события. Возникновение события может привести к выполнению других условий – постусловий события. В качестве примера рассмотрим следующую ниже задачу моделирования.
Пример 3.1. Моделирования системы автомат-продавец.
Автомат-продавец находится в состоянии ожидания до тех пор, пока не появится заказ, который он выполняет и посылает на доставку. Условиями для такой системы являются:
а) автомат-продавец ждет;
б) заказ прибыл и ждет;
в) автомат-продавец выполняет заказ;
г) заказ выполнен.
Событиями для этой системы являются:
1.Заказ поступил.
2. Автомат-продавец начинает выполнение заказа.
3. Автомат-продавец заканчивает выполнение заказа.
4. Заказ посылается на доставку.
Для перечисленных событий можно составить следующую таблицу их пред- и постусловий
|
Событие |
Предусловия |
Постусловия |
|
1 2 3 4 |
нет а. б в г |
б в г. а нет |
›
Такое представление системы легко моделировать сетью Петри. В сети Петри условия моделируются позициями, события — переходами. При этом входы перехода являются предусловиями соответствующего события; выходы — постусловиями. Возникновение события моделируется запуском соответствующего перехода. Выполнение условия представляется фишкой в позиции, соответствующей этому условию. Запуск перехода удаляет фишки, Āпредставляющие выполнение предусловий и образует новые фишки, которые. представляют выполнение постусловий.
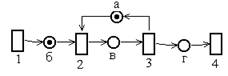 |
ĀĀĀĀĀĀĀĀĀ Пример 3.2. Сеть Петри, моделирующая систему автомат-продавец.
На этом рисунке предусловие выполняется для события 2. ”
Пример 3.3. Моделирование последовательной обработки запросов сервером базы данных. Сервер находится в состоянии ожидания до тех пор, пока от пользователя не поступит запрос, который он обрабатывает и отправляет результат такой обработки пользователю.
Условиями для такой системы являются:
а) сервер ждет;
б) запрос поступил и ждет;
в) сервер обрабатывает запрос;
г) запрос обработан.
Событиями для этой системы являются:
1.Запрос поступил.
2. Сервер начинает обработку запроса.
3. Сервер заканчивает обработку запроса.
4. Результат обработки отправляется.
Таблица пред- и постусловий для перечисленных событий совпадает с аналогичной таблицей для системыĀ автомат-продавец из примера 3.1. Сеть Петри, моделирующая последовательную обработку запросов сервером базы данных, совпадает с аналогичной сетью Петри для системы автомат продавец из примера 3.2..›
Пример 3.4. Моделирование параллельной обработки запросов сервером базы данных. Сервер, как и в примере 3.3, находится в состоянии ожидания до тех пор, пока от пользователя не поступит запрос, который он обрабатывает и отправляет результат пользователю.Ā Отличие состоит в том, что он может обрабатывать одновременно два запроса с помощью двух своих процессорных элементов ПЭ1 и ПЭ2.
Условиями для такой системы являются:
а1) ПЭ1 ждет;
а2) ПЭ2 ждет;
б) запрос поступил и ждет;
в1) ПЭ1 обрабатывает запрос;
в2) ПЭ2 обрабатывает запрос;
г) запрос обработан.
Событиями для этой системы являются:
1.Запрос поступил.
2. ПЭ1 начинает обработку запроса.
3. ПЭ1 заканчивает обработку запроса .
4. ПЭ2 начинает обработку запроса.
5. ПЭ2 заканчивает обработку запроса .
6. Результат обработки отправляется.
Для перечисленных событий можно составить следующую таблицу их пред- и постусловий:
|
Событие |
Предусловия |
Постусловия |
|
1 2 3 4 5 6 |
Нет А1. б В1 А2.б В2 г |
б в1 г. а1 в2 г. а2 нет |
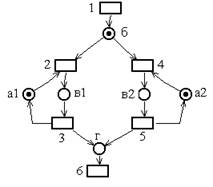 |
Сеть Петри, моделирующая эту систему, имеет вид:
›
3.2. Одновременность и конфликт.
Важная особенность сетей Петри — это их асинхронная природа. В сети Петри отсутствует измерение времени или течение времени. Это отражает философский подход к понятию времени, утверждающий, что важнейшим свойством времени, с является частичное упорядочение событий.Ā При этом считается менее важным протяжённость во времени отдельных событий.
Выполнение сети Петри (или поведение моделируемой системы) рассматривается здесь как последовательность дискретных событий. Порядок появления событий является одним из возможных. Если в какой-то момент времени разрешено более одного перехода, то любой из них может стать ½следующим╗ запускаемым. Тем самым, выбор запускаемого перехода осуществляется недетерминированным образом, т. е. случайно.
Запуск рассматривается как мгновенное событие. Одновременный запуск нескольких различных переходов невозможен. Моделируемое таким образом событие называется примитивным.
Замечание 3.1. Переходы в сети Петри, моделирующей некоторую систему, представляют её примитивные события (длительность которых считается равной 0), и в один момент времени может быть запущен только один разрешённый переход. “
Непримитивними называются такие события, длительность которых отлична от нуля. Они могут пересекаться во времени. Непримитивные события не могут моделироваться переходами. Непримитивное событие может быть промоделировано сетью Петри, например, с помощью двух примитивных событий: ½начало непримитивного события╗, ½конец непримитивного события╗ и условия ½непримитивное событие происходит. Иногда непримитивные события представляют на графе сети Петри в виде большого прямоугольника.
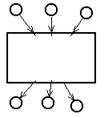 |
Такой прямоугольник может иметь большое значение при моделировании сложных систем на нескольких иерархических уровнях, так как он позволяет выделить в отдельные элементы сети целые подсети, тем самым существенно упростить исходную сеть Петри.
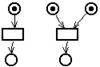 |
Моделирование параллельного возникновения независимых событий системы в сети Петри демонстрируется на следующим рисунке.
В этой ситуации два перехода являются разрешенными и не влияют друг на друга в том смысле, что могут быть запущены один вслед за другим в любом порядке. Такие переходы называются одновременными и моделируют параллельное возникновение событий. Ā
Другая ситуация в приведённой ниже сети Петри. В ней одновременность переходов невозможна.
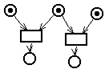 |
Эти два перехода находятся в конфликте, т. е. запуск одного из них удаляет фишку из общей входной позиции и тем самым запрещает запуск другого. Таким образом, моделируются взаимоисключающие события системы.
Замечание 3.2. Области, в которых сети Петри представляются идеальным инструментом для моделирования, характеризуются тем, что в них события происходят асинхронно и независимо. “
3.3. Моделирование аппаратного обеспечения вычислительных систем.
Аппаратное обеспечение вычислительных систем (ВС) можно рассматривать на нескольких уровнях. На низком уровне ВС построены из простых устройств памяти и вентилей; на более высоком уровне в качестве основных компонент системы используются функциональные блоки и регистры. На еще более высоком уровне целые вычислительные системы могут быть компонентами сети ВС. Одним из сильных свойств сетей Петри является их способность моделировать каждый из этих уровней.
3.3.1. Конечные автоматы и их моделирование сетями Петри.
На низком уровне вычислительные системы могут быть описаны автоматами. Автомат—это пятерка (Q,S,D,d,G), где
Q — конечное множество состояний {q1,q2,…,qk};
S — конечный входной алфавит;
D — конечный выходной алфавит;
d: Q´S « Q — функция следующего состояния, отображающая текущее состояние и текущий вход в следующее состояние;
G: Q´S « D — функция выхода, отображающая текущее состояние и текущий вход в выходной символ.
Автоматы часто представляют в виде графов переходов, как, например, на следующем ниже рисунке. В графе переходов состояния представляются кружками, являющимися вершинами. Дуга из состояния q1 в q2 помеченная а/b, означает, что, находясь в состоянии q1, автомат при входе a перейдет в состояние q2, выдавая при этом символ Ь. Формально следовало бы записать d(q1,а)=q2 и G(q1„а)=b.
Пример 3.5. Автомат, вычисляющий чётность количества единиц во входном двоичном числе. Пусть Q={q1,q2} S=D={0,1,R}, где R – признак конца числа (символ сброса). Автомат начинает работу в состоянии q1. Выход копирует вход до тех пор, пока входным символом не окажется
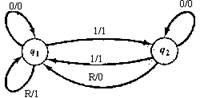 |
символ сброса R. Выходом для символа сброса будет 0 в случае нечетности и 1 — в случае чётности.
Метод моделирования конечных автоматов. Представим каждый входной и выходной символ, а также каждое состояние автомата позицией в сети Петри. Текущее состояние отмечается фишкой; все остальные позиции пусты. Теперь для определения переходов из состояния в состояние можно ввести переходы сети следующим образом. Для каждой пары (состояние, входной символ) мы определяем переход, входными позициями которого являются позиции, соответствующие состоянию и входному символу, а выходными позициями — позиции, соответствующие следующему состоянию и выходу.
Пример 3.6. Сеть Петри, моделирующая автомат из примера 3.5.
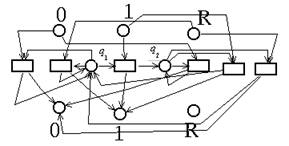 |
Замечание 3.3. Осуществлённое моделирование конечных автоматов сетями Петри показывает возможность применения сетей Петри для разработки аппаратного обеспечения ВС низкого уровня. “
Замечание 3.4.. Одно из основных преимуществ моделей автоматов в виде сетей Петри перед самими автоматами состоит в том, что они существенно упрощают композицию автоматов, как последовательную, так и параллельную. “
Способность сетей Петри моделировать параллелизм и строить модель системы путём довольно простого объединения моделей подсистем делают их весьма полезным инструментом моделирования сложной аппаратуры вычислительных систем.
3.3.2. Конвейерные вычислительные системы и их моделирование сетями Петри.
В последнее время достаточно интенсивно развиваются высокопроизводительные средства параллельной вычислительной техники.Ā К их числу, в частности, относятся вычислительные системы с конвейерной обработкой. Этот метод обработки подобен функционированию сборочного конвейера и особенно удобен для работы с векторами и массивами. Конвейер состоит из набора функциональных устройств (ФУ), которые реализуют различные операции, и могут работать одновременно. Когда операция k завершается, она передает свой результат операции (k + 1) и ожидает от операции (k-1) нового задания. Если каждая операция занимает t единиц времени и всего n операций, то завершение конвейерной обработки одного операнда потребует n*t единиц времени. Однако, если на конвейерную обработку продолжают поступать новые операнды, результаты могут выдаваться со скоростью один в каждые t единиц времени.
Пример 3.6. Конвейер для сложения двух чисел с плавающей точкой. Конвейер образуют следующие операции:
1. Выделить экспоненты обоих чисел.
2. Сравнить экспоненты.
3. Сдвинуть точку в числе с меньшей экспонентой для их уравнения.
4. Сложить дроби.
5. Нормализовать результат.
Этот конвейер позволяет выполнять до пяти сложений одновременно.Ā
Конвейерная обработка может быть синхронной; т. е. время t, отпущенное на выполнение каждой операции, постоянно и является общим для всех ФУ. Каждые t единиц времени результат каждой операции перемещается по конвейеру, чтобы стать входом для следующей операции. Однако при синхронном подходе многие функциональные устройства могут простаивать довольно длительное время из-за того, что требующееся для них время обработки меньше t. В этом случае время t должно определяться самой медленной операцией конвейера, при этом необходимо учитывать, что время выполнения операции зависит от обрабатываемых данных.
Конвейерная обработка также может быть и асинхронной. В асинхронном конвейере процесс обработки может быть ускорен по сравнению с синхронным. Результат операции k асинхронного конвейера может быть послан операции (k+1), как только операция k выполнена, а операция (k+1) свободна. Обычно асинхронный конвейер предполагает наличие регистров. Операция использует значение своего входного регистра для вычисления значения выходного регистра.
При этом ФУ возобновляет свою работу, когда его входной регистр заполнен новым значением, а само ФУ и его выходной регистр свободны. Передача содержимого выходного регистра k-того ФУ во входной регистр k+1-вого ФУ может произойти, если выходной регистр k-того ФУ заполнен, а входной регистр k+1-вого ФУ и само ФУ свободны.
Метод моделирования конвейерной обработки данных. Для моделирования работы k-того ФУ конвейера необходимо выделить следующие условия:
Ę входной регистр k-того ФУ заполнен – (аk);
Ę входной регистр k-того ФУ и само ФУ свободны – (бk);
Ę выходной регистр k-того ФУ заполнен – (вk);
Ę выходной регистр k-того ФУ и само ФУ свободны – (гk);
Ę пересылка осуществляется от k-того ФУ к k+1-вому ФУ – (дk);
Ę
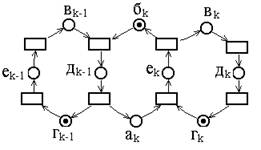 |
k-тое ФУ выполняет операцию – (еk).
Сеть Петри, моделирующая работу k-того ФУ в асинхронном конвейере имеет вид.
Здесь внутренняя работа ФУ и пересылка данных промоделирована, как непримитивные события. Эта модель абстрагируется от внутренней работы ФУ и сосредотачивается на их правильном взаимодействии. Реализуемые с помощью ФУ операции также могут быть промоделированы сетями Петри.
3.3.4. Потоковые системы и их моделирование сетями Петри.
ĀĀĀĀĀĀĀĀĀ Рассмотрим, в качестве примера, один из классов потоковых систем. Пусть потоковая система S=<P,C> определяется множеством процессов P и множеством линий связи C. Множество P разбивается на три подмножества: множество процессов-вычислителей Pcalc, множество процессов ввода Pin и множество процессов вывода Pout. Каждый процесс из Pcalc, имеет конечное ненулевое число входов и выходов. Процессы из Pin Āимеют по одному выходу и ни одного входа, а процессы из Pout. имеют по одному входу и ни одного выхода. Элемент множества C – это линия связи, соединяющая вход и выход некоторых процессов. Каждый вход (выход) процесса связан точно с одним выходом (входом) некоторого процесса.
ĀĀĀĀĀĀĀĀĀ Выходы процессов множества Pin называются входами системы S. Входы процессов множества Pout. называются выходами системы. Система S характеризуется потоками данных на ее входах и выходах.
За каждым выходом процесса pPcalc закреплены условие и функция f. Процесс p вычисляет (![]() ) и f(
) и f(![]() )
)![]() (где
(где ![]() Ā- набор данных,
содержащихся на входах p) и в случае истинности (
Ā- набор данных,
содержащихся на входах p) и в случае истинности (![]() ) помещает результат f(
) помещает результат f(![]() ) на выход, за
которым закреплены и f. Каждый процесс pPcalc, имеет тип, который
определяется четверкой (n,m,
) на выход, за
которым закреплены и f. Каждый процесс pPcalc, имеет тип, который
определяется четверкой (n,m,![]() ,
,![]() ), где n - число входов, m
- число выходов,
), где n - число входов, m
- число выходов, ![]() =<f1,...,fm>
- набор вычисляемых процессом p функций,
=<f1,...,fm>
- набор вычисляемых процессом p функций, ![]() =<1,...,m> - набор условий, удовлетворяющих
следующему ограничению – формула 1...m истинна
=<1,...,m> - набор условий, удовлетворяющих
следующему ограничению – формула 1...m истинна
Каждый процесс pPcalc, может находиться либо в состоянии ожидания, либо в состоянии выполнения. Процесс может перейти из состояния ожидания в состояние выполнения, если все его входы содержат данные и все его выходы свободны. Такой переход сопровождается снятием данных с входов. Процесс может перейти из состояния выполнения в состояние ожидания сразу же, как только результаты вычисления этого процесса будут помещены на его выходы.
Передача данного с выхода вых процесса p на вход вх' процесса-преемника p' может произойти, если процессы p и p' находятся в состоянии ожидания, вых заполнен, а вх' свободен. В этом случае входы могут рассматриваться, как буферы ёмкости 1. Если в качестве входов использовать буферы большей ёмкости, то это повлияет на семантику выполнения потоковой системы следующим образом: Данное может быть принято во входной буфер, если он ещё не заполнен. Принятое данное помещается в конец буферной очереди. При переходе из состояния ожидания в состояние выполнения процесс извлекает из буфера данное, являющееся первым в буферной очереди.
Пример 3.7. Потоковая система, реализующая суммирование элементов матрицы с N=2k столбцами (где k – некоторое целоеĀ положительное число) и произвольным числом строк.
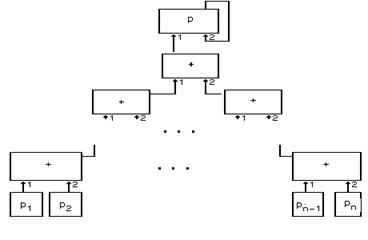 |
В этой системе Pin={ P1, P2,…, Pn }, Pout=Æ. Тип каждого процесса из Pcalc определяется четвёркой (2,1,+,true). Потоки данных на входах системы задаются столбцами матрицы. На входе 2 процесса P происходит накопление суммы. В начальном состоянии на этом входе содержится 0. ŽĀ
Потоковая система в ходе выполнения может войти в тупиковое состояние, в котором обработка входного потока данных ещё не завершена, а система не может продолжать выполнение, из-за невыполнимости для всех процессов условий перехода из состояния ожидания в состояние выполнения. Так потоковая система из примера 3.7 войдёт в тупиковое состояние, если в начальный момент вход 2 процесса P не будет содержать данного.
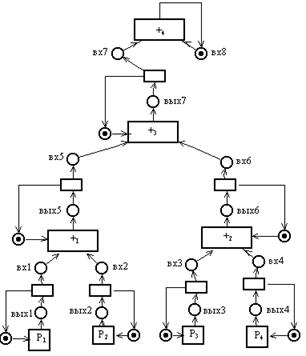 |
ĀĀĀĀĀĀĀĀĀ Пример 3.8. Сеть Петри, моделирующая потоковую систему из примера 3.7 для случая, когда N=4 и и в качестве входов используются буферы неограниченного размера. .
ĀĀĀĀĀĀĀĀĀ В этой сети Петри позиции вх1-вх8 представляют для входов процессов количество данных в соответствующих буферных очередях. Позиции вых1-вых7 представляют для выходов процессов условие ½выход заполнен╗. Непомеченные позиции представляют для процессов условие ½все выходы процесса свободны╗. Переходы P1, P2, P3, и P4 представляют работу процессов ввода, а переходы +1, +2, +3 и +4 представляют работу процессов вычислителей. Непомеченные переходы представляют события передачи данных с выходов одних процессов на входы других.ĀĀ ŽĀ
Метод моделирования потоковой обработки данных.Основную трудность представляет моделирование
функционирования процессов-вычислителей в потоковой системе. В общем случае для
моделирования сетью Петри произвольного процесса pPcalc, имеющего тип (n,m,![]() ,
,![]() ), будем
использовать позиции, представляющие следующие условия:
), будем
использовать позиции, представляющие следующие условия:
Ę Вход процесса заполнен – вхi (для каждого входа 1£i£n процесса);
Ę Выход процесса заполнен – выхi (для каждого выхода 1£i£m процесса);
Ę Процесс находится в состоянии выполнения – вып:
Ę Процесс находится в состоянии ожидания– ожид1 , в котором (m-m(ожид1)) его выходов ещё заполнены.
Ę Процесс находится в состоянии ожиданияĀ и все его выходы пусты – ожид2.
Также будем использовать переходы, представляющие следующие события:
Ę Начало выполнения процесса p - нач
Ę
Завершение выполнения процесса – завi,
1£i£M, (для каждого из M возможных комбинаций
истинных условий из набора ![]() =<1,...,m>,):
=<1,...,m>,):
Ę Передача данного с выхода процесса p (для каждого выхода процесса p).
Ę Завершение передачи данных со всех заполненных выходов процесса p – t.
Сеть Петри, моделирующая функционирования процесса pPcalc, для самого общего случая, в
котором возможна истинность любой комбинации условий из набора ![]() =<1,...,m>, выглядит следующим образом:
=<1,...,m>, выглядит следующим образом:
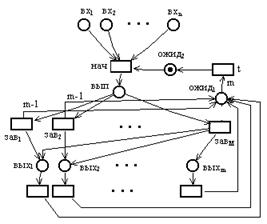 |
Здесь непомеченные переходы представляют события передачи данных с выходов процесса p. Переходы завi (где 1£i£M) являются конфликтными. Запуск одного из них моделирует переход процесса из состояния выполнения в состояние ожидания, который сопровождается заполнением некоторого числа 1£r£m его выходов с истинными условиями. В результате такого запуска помещается по одной фишке в r позиций, соответствующих заполняемым выходам, а в позицию ожид1 помещается (m-r) фишек. Оставшиеся r фишек, необходимых для запуска перехода t, помещаются в эту позицию в результате запусков переходов, представляющих события передачи данных с заполненных выходов процесса p. Ž
3.4. Моделирование программного обеспечения вычислительных систем.
В этом разделе мы покажем, как сети Петри могут моделировать различные системы параллельных взаимодействующих процессов.
3.4.1. Моделирование последовательных процессов.
Вырожденным случаем параллельной системы процессов является система с одним процессом. Сначала рассмотрим, как сетью Петри может быть представлен отдельный процесс, а затем путем комбинации сетей Петри, представляющих несколько процессов, получим модель системы параллельных процессов. Отдельный процесс описывается программой. Эта программа может быть написана на одном из существующих языков программирования.
Пример 3.9. Последовательная программа на абстрактном языке программирования, вычисляющая Y! И произведение всех чётных чисел из отрезка [1,Y] .для произвольного положительного целого Y.
begin
ĀĀ read(Y);
ĀĀ X1:=1;
ĀĀ X2:=1;
ĀĀ while Y>0 do
ĀĀĀĀĀ begin
ĀĀĀĀĀĀĀĀ if mod(Y,2)=0
ĀĀĀĀĀĀĀĀ then begin
ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ X1:=X1*Y;
ĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀĀ end;
ĀĀĀĀĀĀĀĀ X2:=X2*Y;
ĀĀĀĀĀĀĀĀ Y:=Y-1;
ĀĀĀĀĀ end;
ĀĀ write(X1);
ĀĀ write(X2);
endĀĀĀ Ž
Программа представляет два различных аспекта процесса: вычисление и управление. Вычисление связано с текущими арифметическими и логическими операциями, вводом и выводом, обычными манипуляциями над участками памяти и их содержимым. Управление же связано не со значениями или выполняемыми вычислениями, аĀ порядком действий в ходе такого выполнения.
Сети Петри удачно представляют структуру управления программ. Сети Петри предназначены для моделирования упорядочения действий и потока информации, а не для действительного вычисления самих значений. Модель системы в виде сети Петри абстрагируется от характера данных и их преобразований.
Метод моделирования последовательных процессов сетями Петри. Стандартный способ представления структуры программы и потока управления в ней — это блок-схемы. Каждая последовательная программа может быть представлена в виде блок-схемы, которая в свою очередьĀ может быть представлена сетью Петри.Ā
Пример 3.10. Блок-схема программы из примера 3.9.
a:ĀĀ read(Y); X1:=1; X2:=1;
b:ĀĀ Y>0
c:ĀĀ mod(Y,2)=0
d:ĀĀ X1:=X1*Y;
e:ĀĀ X2:=X2*Y; Y:=Y-1;
f:ĀĀ write(X1); write(X2);ĀĀ
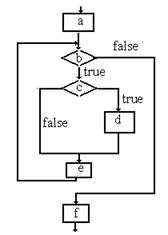 |
Ž
Блок-схема программы состоит изĀ узлов двух типов (принятия решения, обозначаемых ромбами, и вычисления, обозначаемых прямоугольниками) и дуг между ними. В сети Петри действия моделируются переходами, а в блок-схеме действия представляются узлами. Таким образом, в сети Петри, моделирующей блок-схему, узлы блок-схемы представляются переходами сети Петри„ а дуги блок-схемы — позициями сети Петри. Каждая дуга блок-схемы соответствует точно одной позиции в сети Петри. Узлы блок-схемы представляются по разному в зависимости от типа узла: вычисления или принятия решения.
Пример 3.11. Сеть Петри, представляющая блок-схему программы из примера 3.10.Ā
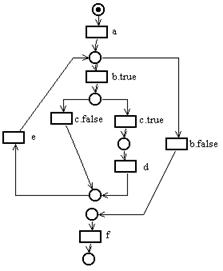 |
Ž
Фишка в сети Петри представляет счетчик команд блок-схемы. Фишка, находящаяся в позиции, означает, что счетчик команд установлен на готовность выполнения следующей команды. Каждая позиция имеет единственный выходной переход, за исключением позиции, которая предшествует принятию решения; такие позиции имеют по два выходных перехода, соответствующих истинному и ложному значению предиката.
Переходы, соответствующие вычислительным узлам блок-схемы, имеют один вход и один выход. Переходы, представляющие действие по принятию решения находятся вĀ конфликте.
3.4.2. Моделирование параллельных систем процессов.
Параллельная система может строиться несколькими способами. Один из способов состоит в простом объединении процессов, без взаимодействия во время их одновременного выполнения. Так, например, если система строится этим способом из двух процессов, каждый из которых может быть представлен сетью Петри, то сеть Петри моделирующая одновременное выполнение двух процессов, является простым объединением сетей Петри для каждого из двух процессов. Начальная маркировка составной сети Петри имеет две фишки, по одной в каждой сети, представляя первоначальный счетчик команд процесса.
Такой способ введения параллелизма имеет низкое практическое значение. Далее будем рассматривать параллельные системы процессов, допускающие взаимодействие процессов во время их параллельного выполнения. Существуют различные виды взаимодействия (синхронизации) процессов, в том числе: взаимодействие посредством общей памяти; - посредством передачи сообщения различных видов. Таким образом, для моделирования сетями Петри параллельных систем процессов, помимо последовательных процессов, необходимо уметь моделировать различные механизмы взаимодействия (синхронизации) процессов. Далее покажем, как сети Петри могут моделировать различные механизмы синхронизации процессов, на основе решения с помощью сетей Петри ряда задач, ставших классическими в области синхронизации.Ā Ā
3.4.3. Задача о взаимном исключении.
Пусть несколько процессов разделяют общую переменную, запись, файл или другой элемент данных. Для обновления разделяемого элемента данных процесс должен сначала считать старое значение, затем вычислить новое и, наконец, записать его на то же место. Если два процесса P1 и P2 в одно и то же время пытаются выполнить такую последовательность действий, то могут возникнуть трудности. Возможна следующая последовательность:
1. Процесс P1 считывает значение из разделяемого объекта;
2. Процесс P2 считывает значение х из разделяемого объекта;
3. Процесс P1 вычисляет новое значение х'=f(x);
4. Процесс P2 вычисляет новое значение х"=g(x);
5. Процесс P1 записывает х' в разделяемый объект;
6. Процесс P2 записывает х" в разделяемый объект, уничтожая значение х
Результат вычисления процесса P1 потерян.
Теперь значением разделяемого объекта является g(x);в то время как им должно быть либо g(f(x)), либо f(g(x)). Очевидно, что это должно быть так, например, в случае, когда g(x)Ā — ½снять со счета х 1000 долл.╗, f(x) — ½поместить на счет х 1000 дол.╗, а процессы P1 и P2 — банковские операции.
Для исключения подобных проблем используется метод взаимного исключения, основанный на понятии критическая секция. Критическая секция – это участок кода процесса, на котором он осуществляет доступ к разделяемому объекту данных. Прежде, чем выполнить свою критическую секцию, процесс ждёт, пока другой процесс не закончит выполнение собственной критической секцииĀ (если такое выполнение имеет место). Затем он входит в критическую секцию и блокирует доступ для любого другого процесса к своей критической секции. После выполнения процессом критической секции деблокируется доступ для других процессов к разделяемому объекту данных.
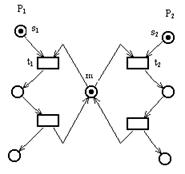 |
Следующая ниже сеть Петри моделирует механизм взаимного исключения для двух процессов P1 и P2. Она легко обобщается на произвольное число процессов.
Позиция m представляет условие ½критическая секция свободна╗, разрешающее вход в критическую секцию. Попытка процесса P1 (P2) войти в критическую секцию осуществляется после помещения фишки в его позицию s1 (s2). Такая попытка может увенчаться успехом, если в позиции m содержится фишка. Если оба процесса пытаются войти в критическую секцию одновременно, то переходы t1 и t2 вступят в конфликт, и только один из них сможет запуститься. Запуск t1 запретит запуск перехода t2, вынуждая процесс P2 ждать, пока процесс P1 выйдет из своей критической секции, и возвратит фишку обратно в позицию m.
3.4.4. Задача о производителе/потребителе.
В задаче о производителе/потребителе также присутствует разделяемый объект – буфер, посредством которого реализуется взаимодействие через асинхронную передачу сообщений. Процесс-производитель создает сообщения, которые помещаются в буфер. Потребитель ждет, пока сообщение не будет помещено в буфер, извлекает его оттуда и использует. Такое взаимодействие может быть промоделировано следующей ниже сетью Петри.
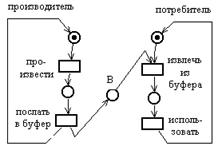 |
Позиция B представляет буфер, каждая фишка соответствует сообщению, которое произведено, но еще не использовано.
В другом варианте этой задачи несколько производителей порождают сообщения, помещаемые в общий буфер, для нескольких потребителей. Моделирующая сеть Петри для этого варианта совпадает с сетью для предыдущего варианта задачи, за исключением того, что для представления s производителей и t потребителей используются sĀ фишек в начальной позиции процесса-производителя и t фишек в начальной позиции процесса-потребителя.
Ещё в одном варианте задачи о производителе/потребителе используется буфер ограниченного размера, имеющий n ячеек для временного хранения сообщений. Здесь возможна ситуация, когда производитель будет вынужден ждать, если потребитель работает медленно и буфер заполнен. Для этого варианта задачи моделирующая сеть Петри выглядит следующим образом:
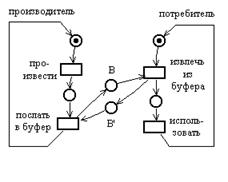 |
Ограниченному буферу сопоставляются две позиции: B представляет количество сообщений, которые произведены, но еще не использованы (число заполненных ячеек), и B' — количество пустых ячеек в буфере. Первоначально B' имеет n фишек, а B фишек не имеет. Если буфер заполнен, то B' фишек не имеет, а B имеет n фишек. Если теперь производитель попытается поместить еще одно сообщение в буфер, то он будет остановлен, так как в B' нет фишек.
3.4.5. Задача об обедающих мудрецах.
Задача об обедающих мудрецах была предложена Дейкстрой и связана с пятью мудрецами, которые попеременно то думали, то ели. Мудрецы сидят за круглым столом, на котором много блюд китайской кухни. Между соседями лежит одна палочка для еды. Для приема китайской пищи необходимо две палочки. Поэтому каждый мудрец должен сначала взять палочку слева и палочку справа, а затем приступать к еде. Возможна ситуация, в которой каждый мудрец возьмёт палочку слева, а затем будет ждать, когда освободится палочка с правой стороны. Так они будут ждать, пока не умрут от голода. Тем самым, это состояние системы ½обедающие мудрецы╗ является тупиковым.
Проблема тупика в этой системе может быть решена путём следующей модификации её правил поведения: Пусть мудрец при переходе из состояния размышления в состояние приёма пищи захватывает, не по очереди, а одновременно обе палочки (слева и справа), если они свободны. Следующая ниже сеть Петри моделирует такую
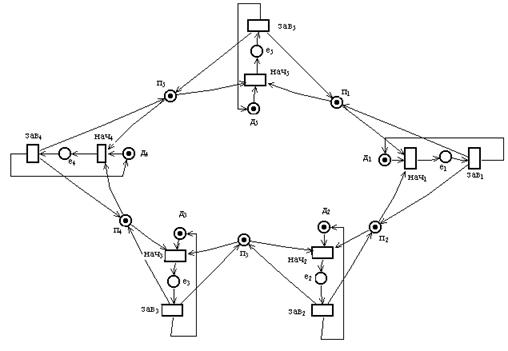 |
модифицированную систему обедающих мудрецов, свободную от тупиков.
В этой сети Петри позиция пi, iÎ{1,2,3,4,5}, представляет условие ½i-тая палочка свободна╗. В начальной маркировке каждая из этих позиций имеет фишку. Каждому мудрецу iÎ{1,2,3,4,5} соответствует две позиции: позиция дi – представляющая условие ½i-тый мудрец думает╗; и позиция еi. – представляющая условие ½i-тый мудрец ест╗. В начальной маркировке каждая позиция дi содержит фишку, а каждая позиция еi пуста.
Каждому мудрецу iÎ{1,2,3,4,5} также соответствует два перехода: переход начi – представляющий событие ½начало приёма пищи i-тым мудрецом╗; и переход завi – представляющий событие ½завершение приёма пищи i-тым мудрецом╗.
Замечание 3.5. В системе ½обедающие мудрецы╗ мудрецы могут интерпретироваться, как последовательные процессы, а палочки, как разделяемые ресурсы, посредством которых эти процессы взаимодействуют. Ž
3.4.6. Задача о чтении/записи.
Имеются процессы двух типов: процессы чтения и процессы записи. Все процессы совместно используют общий элемент данных. Процессы чтения не изменяют элемент данных в отличие от процессов записи. Таким образом, процессы записи должны взаимно исключать все другие процессы чтения и записи. При этом несколько процессов чтения могут иметь доступ к разделяемым данным одновременно. Задача состоит в определении структуры управления, которая не приведет к тупику и не допустит нарушения механизма взаимного исключения.
Пусть имеются s процессов чтения и t процессов записи, а количество одновременно работающих процессов чтения ограничено величиной n. Моделирующая сеть Петри в этом случае имеет вид:
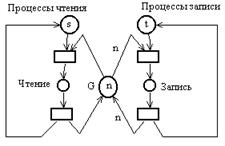 |
В этой сети позиция ½Чтение╗ представляет количество одновременно работающих процессов чтения. При инициализации каждого процесса чтения в эту позицию добавляется фишка, а по окончании процесса чтения фишка удаляется из неё. С помощью позиции G реализуется ограничение на количество одновременно работающих процессов чтения, а так же – разрешение на запуск процесса записи (в начальный момент она содержит n фишек). Инициализация процесса записи возможна, если в позиции G находится n фишек (т.е. ни один из процессов не работает). В результате запуска такого процесса из позиции G все n фишек удаляются, тем самым блокируется возможность запуска для любого другого процесса. По окончании работы процесса записи n фишек возвращаются в позицию G.
Одним из самых популярных механизмов синхронизации процессов являются P- и V-операции над семафорами, впервые определенные Дейкстрой. Семафор — это элемент данных, который может принимать только неотрицательные целые значения. V-операция увеличивает значение на 1, а P-операция уменьшает его на 1. P-операцию можно применять только в том случае, когда значение семафора останется в результате неотрицательным; если же значение семафора равно 0, то P-операция должна ждать, пока какой-нибудь другой процесс не выполнит V-операцию. P- и V-операции определены как примитивные, т. е. никакая другая операция не может изменять значение семафора одновременно с ними. Такие операции легко моделируются сетью Петри, как показано ниже.
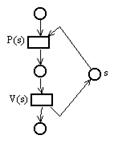 |
Каждый семафор s моделируется позицией s, количество фишек в этой позиции показывает значение семафора. P-операция использует позицию семафора в качестве входа, V-операция — в качестве выхода.
Многие системы проектируются и описываются с помощью P - и V-операций, например, операционные системы. Такие системы, следовательно, можно промоделировать сетями Петри.
3.5. Примеры моделирования локальных компьютерных сетей.
В настоящее время Сети Петри наиболее интенсивноĀ используются для моделирования и анализа протоколов передачи данных. В компьютерных сетях и распределенных системах процессов необходима корректная организация передачи информации между компьютерными узлами, процессами. На данный момент разработано рядĀ методологий для проектирования, спецификации и анализа протоколов, на основе сетей Петри и подобных им моделях.
Рассмотрим ряд примеров моделирования передачи сообщений в локальных компьютерных сетях с различными топологическими структурами связей.Ā
Пример 3.12. Локальная сеть с линейной топологиейĀ и двумя компьютерными узламиĀ КУ1 и КУ2. Рассмотрим работу этой сети на следующем уровне абстракции. Функционирование системы состоит в обмене сообщениями между узлами КУ1 и КУ2. Каждый узел может находиться в одном из состояний: состоянии готовности к передаче сообщения, и состоянии готовности к приёму сообщения. Передача сообщения от одного узла к другому может произойти, если один из них находится в состоянии готовности к передаче сообщения, другой – в состоянии готовности к приёму сообщения,
Для моделирования такой системы будем использовать следующие условия:
Ę КУi готов к передаче сообщения – гперi (для iÎ{1,2});
Ę КУ1 готов к приёму сообщения – гпрi;
Ę Происходит передача сообщения от КУ1 к КУ2 – пер1;Ā
Ę Происходит передача сообщения от КУ2 к КУ1 – пер2.
Выделим также в системе следующие события:
Ę КУi переходит из состояния готовности к передаче сообщения в состояние готовности к приёму сообщения –Ā аi (для iÎ{1,2});
Ę КУi переходит из состояния готовности к приёму сообщения в состояние готовности к передаче сообщения –Ā бi
Ę КУi отправляет сообщение – отпi;
Ę КУi получает сообщение – полi.
Моделирующая сеть Петри имеет следующий вид:
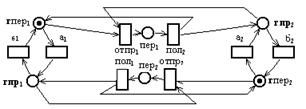 |
Маркировка этой сети Петри представляет состояние системы в котором узел КУ1 готов к передаче сообщения, узел КУ2 готов к приёму сообщения. Разрешёнными являются три перехода отп1, а1, и б2. В результате запуска перехода отп1;(инициализации передаче сообщения от узла КУ1 к узлу КУ2.) фишка будет находиться только в позиции пер1, и разрешённым станет только переход полi2;Ā В результате запуска этого перехода полi2 сеть перейдёт в первоначальное состояние. Запуск переходов а1, и б2 может привести к передаче сообщения от узла КУ2 к узлу КУ1.‡
Пример 3.13. Моделирование локальной сети из примера 3.12 модифицированной требованием справедливости её поведения. Требование справедливости поведения состоит в следующем: Пусть количество подряд передаваемых сообщений для каждого узла КУ1 и КУ2 не превышает некоторого положительного целого N. Передача сообщения от одного узла к другому может произойти, если один из них находится в состоянии готовности к передаче сообщения, другой – в состоянии готовности к приёму сообщения, и количество подряд посланных сообщений для передающего узла не превышает N.
Для моделирования такой системы дополнительно, по сравнению с примером 3.12, будем использовать позиции пi (где iÎ{1,2}), каждая из которых представляетĀ количество переданных подряд сообщенийĀ для узлаĀ КУ1.
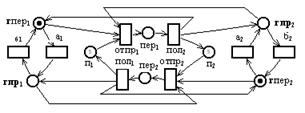 |
В начальный момент в позиции п1 и п2 помещаются N фишек. Моделирование передачи одного сообщения от узла КУ1 к узлу КУ2 удаляет одну фишку из позиции п1 посредством запуска перехода отп1 и помещает одну фишку в позицию п2 посредством запуска перехода пол2. Тем самым общее количество фишек в позициях п1 и п2 остаётся равным N,, а моделирование передачи сообщений от узла КУ1 к узлу КУ2 может повторяться до тех пор, пока позиция п1 не станет пустой. Количество таких повторений не превосходит N, т.кĀ исходное. количество фишек в позиции п1 не превосходит N. То же самое справедливо и по отношению к моделированию передачи сообщений от узла КУ2 к узлу КУ1.
3.6. Моделирование железнодорожного движения на основе сетей Петри.
ĀĀĀĀĀĀĀĀĀ Сначала покажем, как можно моделировать сетью Петри работу железнодорожного узла. Пусть система ½железнодорожный узел╗ (ЖУ) включает в себя конечное число N путей и соответствующие им семафоры. В него с северного и южного направлений могут прибывать поезда, а также – отправляться по этим же направлениям. Прибывший поезд может быть принят на один из свободных путей.
Для построения модели системы ЖУ в виде сети Петри выделим в ней следующие условия:
Ę Поезд прибывает с северного направления (обозначим это условие через Сin);
Ę Поезд прибывает с южного направления (Юin);
Ę Поезд отправился в с северном направлении (Сout);
Ę Поезд отправился в южном направлении (Юout);
Ę На k-том (где 1£k£N) пути находится поезд (Пk);
Ę Семафор, соответствующий k-тому пути даёт зелёный свет (Зk).
С этой же целью в системе ЖУ выделим следующие события:
Ę Поезд, прибывший с северного направления, принимается на k-тый путьĀ (СПk);
Ę Поезд, прибывший с южного направления, принимается на k-тый путьĀ (ЮПk);
Ę Поезд отправляется с k-того пути в северном направлении (ОСk);
Ę Поезд отправляется с k-того пути в южном направлении (ОЮk);
Определим пред- и постусловия событий в этой системе.
|
Событие |
Предусловия |
Постусловия |
|
СПk ЮПk ОСk ОЮk |
Сin, Зk Юin, Зk Пk Пk |
Пk Пk Сout Юout |
›
Следующая нижеĀ сеть Петри моделирует систему ЖУ для случая N=2.
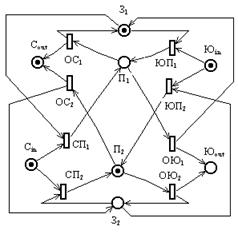 |
В этой сетиĀ маркировка соответствует состоянию системы ЖУ, в котором поезд прибывает с северного и с южного направлений, в северном направлении отправился поезд, первый путь свободен, а второй путь занят. Эта сеть Петри легко может быть достроена для произвольного фиксированного N>2. Методы анализа сетей Петри позволяют устанавливать автоматически интересные с практической точки зрения свойства логической корректности моделируемых систем. Для рассматриваемой системы ЖУ, с их помощью, в частности, можно установить, что система никогда не войдёт в тупик, т.е. в такое состояние, в котором ни один из поездов не может продолжить движение. Также можно обосновать, что организация работы этой системы не допускает ситуации, при которой два поезда одновременно направляются на один и тот же путь.
Теперь рассмотрим железнодорожную сеть ЖС, которая образованна двумя железнодорожными узлами ЖУ, ЖУ’ и перегоном между ними. Перегон определяется двухколейной железной дорогой. Узлы ЖУ и ЖУ’ содержат N и N’ путей соответственно. Для моделирования железнодорожную сеть ЖС будем использовать: 1) сети Петри, моделирующие узлы ЖУ и ЖУ’; 2) позиции К и К’, представляющие количество поездов на перегоне, для каждого из двух направлений движения на перегоне; а также переходы вх, вых, вх’ и вых’, моделирующие вход поезда в зону железнодорожного узла и выход из зоны железнодорожного узла для узлов ЖУ и ЖУ’.
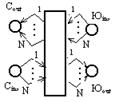 |
Сеть Петри, моделирующую узел ЖУ будем использовать в следующем виде:
Здесь внутренняя работа узла скрыта прямоугольником, асвязь с внешним миром будет осуществляться с помощью позиций Сin, Юin, Сout, и Юout,. Сеть Петри, моделирующая железнодорожную сеть ЖС имеет следующий вид:Ā
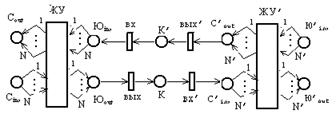 |
Заметим, что система ЖС допускает произвольное количество поездов на перегоне для каждого направления движения, а позиции К и К’ моделирующей ети Петри могут содержать произвольное число фишек. В реальной железнодорожной сети количество поездов на перегоне ограниченно, в частности, минимально допустимым расстоянием между поездами, движущимися в одном направлении. Покажем, как модифицировать моделирующую сеть Петри, чтобы она описывала систему ЖС с ограниченным количеством поездов на перегоне. Для этого в приведённой выше сети Петри выделим подсети моделирующие движение поездов от одного железнодорожного узла к другому для каждого направления движения и достроим эти подсети так, как показано ниже на примере движения в южном направлении. Подсеть, моделирующая движение поезда в южном направлении, от узла ЖУ к узлу ЖУ’, имеет вид:
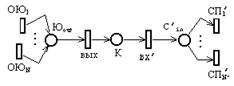 |
Достроим эту сеть Петри следующим образом:
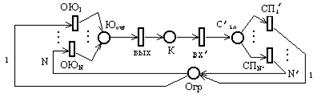 |
В начальный момент позиция Огр содержит число фишек, совпадающее с максимально допустимым количеством поездов z на рассматриваемом перегоне, а позиция К пуста. Запуск любого перехода, моделирующего отправление поезда из узла ЖУ, удаляет одну фишку из позиции Огр одну фишку. Запуск любого перехода, моделирующего прибытие поезда в узел ЖУ’, добавляет одну фишку в эту позицию. Если на перегоне находится z поездов, то позиция Огр будет пустой, а запуск перехода, моделирующего отправление поезда не возможен.
Методы анализа сетей Петри позволяют автоматически устанавливать, что количество поездов на перегоне удовлетворяет соответствующему ограничению.
Детализация и уточнение моделирующей сети Петри для железнодорожной сети ЖС может быть продолжена.
Моделирование систем сетями Петри, прежде всего, обусловлено необходимостью проведения глубокого исследования их поведения. Для проведения такого исследования необходимы методы анализа свойств самих сетей Петри. Этот подход предполагает сведения исследования свойств реальной системы к анализу определённых свойств моделирующей сети Петри. В этом разделе определим основные свойства сетей Петри, продемонстрируем их практическое значение, а также приведём соответствующие методы анализа.
Безопасность. Одно из важнейших свойств сети Петри — это безопасность. Позиция сети Петри является безопасной, если число фишек в ней никогда не превышает 1
Определение 4.1. Позиция pÎP сети Петри N=(P,Т,I,O) c начальной маркировкой m является безопасной, если m’(p)£1 дляĀ любой достижимой маркировки m’ÎR(N,m) (где R(N,m) – множество достижимых маркировок из начальной маркировки m в сети Петри N). . Сеть Петри безопасна, если безопасны все позиции сети. Ž
Замечание 4.1. Сеть Петри может быть преобразована в безопасную, если все её позиции в начальной маркировке являются безопасными и их входная и выходная кратность равна 0 или 1 для всех переходов. Ž
Практическое значение свойства безопасности, в том числе, заключается в следующем. Безопасность — очень важное свойство для устройств аппаратного обеспечения. Если позиция безопасна, то число фишек в ней равно 0 или 1. Следовательно, эту позицию можно реализовать одним триггером.
К анализу свойства безопасности позиций моделирующей сети Петри может быть сведено исследование, например, таких свойств ранее рассмотренных систем, как: Отсутствие потери данных в асинхронном конвейере при передаче от одного функционального устройства к другому (т.е. помещение новых данных во входные и выходные регистры функциональных устройств только после того, как эти регистры будут освобождены от старых данных). Аналогичное свойство для параллельных систем процессов, взаимодействующих посредством передачи сообщений и использующих для этого буфер ёмкости один. Свойство организации работы железнодорожного узла, исключающее ситуацию, при которой на одном пути оказываются более одного поезда. (Позиции, представляющие состояние регистров, буферов и путей в соответствующих моделирующих сетях Петри должны быть безопасными).
Ограниченность. Безопасность — это частный случай свойства ограниченности. Позиция является k-ограниченной, если количество фишек в ней не может превышать целое число k.
Определение 4.2. Позиция pÎP сети Петри N=(P,Т,I,O) c начальной маркировкой m является k-ограниченной, если m’(p)£k дляĀ любой достижимой маркировки m’ÎR(N,m). Позиция называется ограниченной, если она является k-ограниченной для некоторого целого значения k. Сеть Петри ограниченна, если все ее позиции ограниченны. Ž
Практическое значение свойства ограниченности, в частности, состоит в следующем. Ограниченную сеть Петри можно реализовать аппаратно. При этом для аппаратной реализации ограниченной позиции можно использовать электронное устройство – счётчик. Сеть Петри с неограниченными позициями в общем случае реализовать аппаратно нельзя.
Ограниченность позиций моделирующей сети ПетриĀ может гарантировать отсутствие потери данных из-за переполнения буфера (ограниченного размера) в параллельных системах процессов, взаимодействующих посредством передачи сообщений. Позиция, представляющая количество сообщений в буфере, должна быть k-ограниченной, где k – размер буфера. Свойство ограниченности позиций моделирующей сети Петри для железнодорожной сети может гарантировать, что количество поездов на перегоне удовлетворяет соответствующему ограничению. Позиция, представляющая количество поездов на перегоне, должна быть z-ограниченной , где z – максимально допустимое число таких поездов.
Сохранение. Практическая мотивация введения свойства сохранения, в частности, состоит в следующем. Сети Петри можно использовать для моделирования систем распределения ресурсов. В этих системах фишки могут представлять ресурсы. Для сетей Петри, моделирующих такие системы, важным свойством является сохранение, гарантирующее, что фишки, представляющие ресурсы, никогда не создаются и не уничтожаются. Т.е. общее их число в сети остаётся постоянным.
Определение 4.3. Сеть Петри N=(P,Т,I,O) с начальной маркировкой m является строго сохраняющей, если дляĀ любой достижимой маркировки m’ÎR(N,m) справедливо следующее .
![]() m’(p) =
m’(p) =
![]() m(p).
Ž
m(p).
Ž
Замечание 4.2. Строгое сохранение — это сильное ограничение, из которого следует, что число входов в каждый переход должно равняться числу выходов из него. Ž
В общем случае взаимно однозначного соответствия между
фишками и ресурсами может не быть. Фишка может представлять несколько ресурсов
сразу. Такая фишка позже используется для создания кратных фишек (по одной на
ресурс) путем запуска перехода с большим числом выходов, чем входов. В связи с
этим в общем случае свойство сохранения требует, чтобы взвешенная сумма
для всех достижимых маркировок была постоянной. При этом используется вектор взвешивания
![]() =<1,...,m> который, определяет для каждой
позиции piÎP. вес i находящейся в ней фишки, где i целые неотрицательные числа, п=\P\.
Если i=0, то фишки, находящиеся
в позиции pi, являются несущественными.
=<1,...,m> который, определяет для каждой
позиции piÎP. вес i находящейся в ней фишки, где i целые неотрицательные числа, п=\P\.
Если i=0, то фишки, находящиеся
в позиции pi, являются несущественными.
Определение 4.4. Сеть Петри N=(P,Т,I,O) с
начальной маркировкой m является сохраняющей по отношению к вектору
взвешивания ![]() =<1,...,m>, если дляĀ любой достижимой
маркировки m’ÎR(N,m) справедливо .
=<1,...,m>, если дляĀ любой достижимой
маркировки m’ÎR(N,m) справедливо .
![]() i
*m’(pi) =
i
*m’(pi) = ![]() i
*m(pi).
Ž
i
*m(pi).
Ž
Сеть Петри называется сохраняющей, если она
сохраняющая по отношению к некоторому ненулевому вектору взвешивания ![]() . Свойство
сохранения, в частности, может гарантировать для заданной железнодорожной сети,
чтоĀ количество, находящихся в ней поездов, не изменяется.
. Свойство
сохранения, в частности, может гарантировать для заданной железнодорожной сети,
чтоĀ количество, находящихся в ней поездов, не изменяется.
Активность. Другая задача, которая возникает при распределении ресурсов— это обеспечение отсутствия тупиков. В качестве примера, рассмотрим систему, включающую в себя два ресурса q и r, разделяемые двумя процессами a и b. Циклический процесс a на каждой итерации цикла сначала запрашивает ресурс q, затем ресурс r и, наконец, освобождает и q, и r. Процесс b работает аналогично, но сначала запрашивает r, а затем q. Следующая ниже сеть Петри моделирует эту систему.
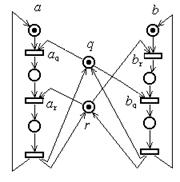 |
Последовательность запусков переходов aq,, br, приводит к тупику. В этой ситуации процесс a обладает ресурсом q и хочет получить r, процесс b обладает r и хочет получить q. Ни один из процессов не может продолжать выполнение из-за занятости необходимого ресурса другим процессом.
Тупик в сети Петри — это переход (или множество переходов), которые не могут быть запущены. В связи с понятием тупика определим для сети Петри N с начальной маркировкой m следующие уровни активности переходов:
Уровень 0: Переход t обладает активностью уровня 0, если он никогда не может быть запущен.
Уровень 1: Переход t обладает активностью уровня 1, если он потенциально запустим, т. е. если существует такая m’ÎR(N,m), что t разрешён в m’.
Уровень 2: Переход t обладает активностью уровня 2, если для всякого целого n существует последовательность запусков, в которой t присутствует по крайней мере n раз.
Уровень 3: Переход t обладает активностью уровня 3, если существует бесконечная последовательность запусков, в которой t присутствует неограниченно часто.
Уровень 4: Переход t, обладает активностью уровня 4, если для всякой m’ÎR(N,m) существует такая маркировка m”ÎR(N,m’), что t разрешен в m”.
Переход, обладающий активностью уровня 0, называется пассивным. Переход, обладающий активностью уровня 4, называется активным.
Достижимость и покрываемость. Определение 4.5. Задача достижимости. Для данной сети Петри с маркировкой mĀ и маркировки m’ определить: m’ÎR(N,m)?
Многие другие задачи анализа можно сформулировать в терминах задачи достижимости. В частности, если известно, что маркировка описывает тупик в сети Петри, то возникает вопрос о её достижимости из начальной маркировки.Ā
Определение 4.6. Задача покрываемости. Для данной сети Петри N с начальной маркировкой m и маркировки m’ определить, существует ли такая достижимая маркировка m”ÎR(N,m), что m">³m’. Ž
(Отношение m"³m’ истинно, если каждый элемент маркировки m" не меньше соответствующего элемента маркировки m’.)
Многие задачи анализа активности переходов могут быть сведены к исследованию покрываемости. При этом существенное значение имеет тот факт, что разрешённость перехода в маркировке m", следует из разрешённости перехода в маркировке m’ если m"³m’.
Последовательности запусков переходов. Другой подход к анализу основан не на позициях, а на последовательностях запусков переходов. В общем случае ставится следующая задача: Для заданной сети Петри определить, возможна ли заданная последовательность запусков переходов или возможна ли какая-либо последовательность из заданного множества последовательностей запусков переходов. Такая задача актуальна, например, в случае, когда известно, что заданная последовательность запусков переходов приводит к тупику или нарушает взаимное исключение процессов.
Эквивалентность и включение. Сети Петри присуще некоторое поведение, которое определяется множеством её возможных последовательностей запусков переходов или её множеством достижимых маркировок. Интересной с практической точки зрения является задача оптимизации (изменения) сети Петри без изменения её поведения. Изменение означает, в частности, удаление пассивных переходов (которые никогда нельзя запустить), или пассивных позиций (которые никогда не могут быть маркированы). Оптимизация может состоять, в частности, в увеличении параллелизма, в уменьшении стоимости аппаратной реализации. Понятие эквивалентности сетей Петри может быть определено через равенство множеств достижимых маркировок.
Определение 4.7. Сеть Петри N=(P,Т,I,O) с начальной маркировкой m иĀ сеть Петри N’=(P’,Т’,I’,O’) с начальной маркировкой m’ эквивалентны, если справедливо R(N,m)=R(N’,m’). Ž
Понятие эквивалентности сетей Петри может быть определено также через равенство множеств возможных последовательностей запусков переходов. Более слабым , по сравнению с эквивалентностью, является свойство включения.
Определение 4.8. Сеть Петри N=(P,Т,I,O) с начальной маркировкой m является включением сети Петри N’=(P’,Т’,I’,O’) с начальной маркировкой m’, если справедливо R(N,m)ÍR(N’,m’). Ž
4.2. Методы анализа.
Особый интерес вызывают методы анализа свойств сетей Петри, которые обеспечивают автоматический анализ моделируемых систем. В этом разделе мы представим два основных метода анализа сетей Петри, которые позволяют решать некоторые из перечисленных в предыдущем разделе задач. Первый метод анализа основан на использовании дерева достижимости, а второй метод – на решении матричных уравнений.
4.2.1. Дерево достижимости.
Дерево достижимости представляет все достижимые маркировки сети Петри, а также – все возможные последовательности запусков её переходов.
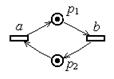 |
Пример 4.1. Частичное дерево достижимости маркированной сети Петри. Сеть Петри имеет вид:
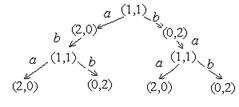 |
Частичное дерево достижимости для трёх шагов построения имеет вид:
•
Шаг построения дерева достижимости состоит в добавлении к каждой граничнойĀ вершине-маркировке веера, образованного множеством всех маркировок, непосредственно достижимых из данной граничной маркировки. На первом шаге граничной является вершина, соответствующая начальной маркировке. Каждая дуга помечена запускаемым переходом, при переходе из одной маркировки в другую. Всякий путь в дереве, начинающийся в корне, соответствует допустимой последовательности переходов.
Для сети Петри с бесконечным множеством достижимых маркировок дерево достижимости является бесконечным. Сеть Петри с конечным множеством достижимых маркировок также может иметь бесконечное дерево достижимости (см. пример 4.1). Для превращения бесконечного дерева в полезный инструмент анализа строится его конечное представление. При построении конечного дерева достижимости для обозначения бесконечного множества значений маркировки позиции используется символ w. Также используются следующие ниже операции над w, определяемые для любого постоянного a.
w --а = w;ĀĀ w + а = w;ĀĀ а < w;ĀĀ w £ w.
Алгоритм построения конечного дерева достижимости. Каждая вершина дерева достижимости классифицируется алгоритмом или как граничная вершина, терминальная вершина, дублирующая вершина, или как внутренняя вершина. Алгоритм начинает работу с определения начальной маркировки корнем дерева, и граничной вершиной. Один шаг алгоритма состоит в обработке граничной вершины. Пусть х — граничная вершина, тогда её обработка заключается в следующем:
1. Если в дереве имеется другая вершина y, не являющаяся граничной, и с ней связана та же маркировка, m[x]=m[y], то вершина х становится дублирующей.
2. Если для маркировкиĀ m[х]Ā ни один из переходов не разрешен, го
x становится терминальной.
3. В противном случае, для всякого перехода tÎT, разрешенного в m[х], создаётся новая вершина z дерева достижимости. Маркировка m[z], связанная с этой вершиной, определяется для каждой позиции pÎP следующим образом:
3.1. Если Ām[х](p)=w, то m[z](p)=w.
3.2. Если на пути от корневой вершины к x существует вершина y с m[y]<m’ (где m’ – маркировка, непосредственно достижимая из m[х] посредством запуска перехода t) и m[y](p)<m’(p), то m[z](p)=w. (В этом случае последовательность запусков переходов, ведущая из маркировки m[y] в маркировку m’, может неограниченно повторяться и неограниченно увеличиватьĀ значение маркировки в позиции p.) В противном случае m[z](p)=m’(p).
4. Строится дуга с пометкой t, направленная от вершины x к вершине z. Вершина х становится внутренней, а вершина z – граничной.
Такая обработка алгоритмом граничных вершин продолжается до тех пор, пока все вершины дерева не станут терминальными, дублирующими или внутренними. Затем алгоритм останавливается.
Замечание 4.3. Важнейшим свойством алгоритма построения конечного дерева достижимости является то, что он за конечное число шагов заканчивает работу. Ž
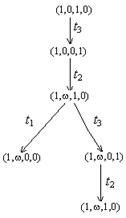
Пример 4.2. Конечное дерево достижимости сети Петри.
Сеть Петри:
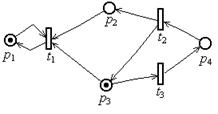 |
Конечное дерево достижимости:
 |
“
Алгоритм построения конечного дерева достижимости был впервые описан Карпом и Миллером. Ими же была доказана конечность дерева достижимости (завершение этого алгоритма). Ниже приводится один из вариантов такого доказательства.
Лемма 4.1. В любом бесконечном направленном дереве, в котором каждая вершина имеет только конечное число непосредственно последующих вершин, существует бесконечный путь, исходящий из корня. “
Доказательство. Пусть x0 корневая вершина. Поскольку имеется только конечное число непосредственно следующих за x0 вершин, но общее число вершин в дереве бесконечно, по крайней мере, одна из непосредственно следующих за x0 вершин должна быть корнем бесконечного поддерева. Выберем вершину x1 непосредственно следующую за x0 и являющуюся корнем бесконечного поддерева. Теперь одна из непосредственно следующих за ней вершин также является корнем бесконечного поддерева, выберем в качестве такой вершины x2. Если продолжать этот процесс бесконечно, то получим бесконечный путь в дереве – x0,x1,x2,…,xn,… . “
Лемма 4.2. Всякая бесконечная последовательность неотрицательных целых содержит бесконечную неубывающую последовательность. “
Доказательство. Возможны два случая:
1. Если какой-либо элемент последовательности встречается бесконечно часто, то пусть x0 является таким элементом. Тогда бесконечная подпоследовательность x0,x0,…,x0,… является бесконечной неубывающей подпоследовательностью.
2. Если никакой элемент не встречается бесконечно часто, тогда каждый элемент встречается только конечное число раз. Пусть x0 — произвольный элемент последовательности. Существует самое большее x0 целых, неотрицательных чисел (0,..., x0-1), меньших, чем x0, причем каждый из них присутствует в последовательности только конечное число раз. Следовательно, продвигаясь достаточно долго по последовательности, мы должны встретить элемент x1, x1 ³ x0. Аналогично за x1 должен существовать в последовательности элемент x2, x2 ³ x1, и т. д. Это определяет бесконечную неубывающую последовательность x0,x1,x2,…,xn,… .
Таким образом, в обоих случаях бесконечная неубывающая подпоследовательность существует. —
Лемма 4.3. Всякая бесконечная последовательность n-векторов над расширенными символом w неотрицательными целыми содержит бесконечную неубывающую подпоследовательность. “
Доказательство. Доказываем индукцией по n, где n — размерность векторного пространства.
1. Базовый случай (n=1). Если в последовательности имеется бесконечное число векторов вида <w>, то они образуют бесконечную неубывающую последовательность (так как справедливо w£w). В противном случае бесконечная последовательность, образованная удалением конечного числа экземпляров <w>, имеет по лемме 4.2 бесконечную неубывающую подпоследовательность.
2. Индуктивное
предположение. (Допустим, что лемма верна для n,
докажем её справедливость для n+1.) Пусть согласно предположению в исходной
последовательности n+1-векторов содержится подпоследовательность
![]() ,
, ![]() ,…
Ā, неубывающая по каждой из
первых n
координат. Рассмотрим n+1-вую координату в этой
последовательности. Если в последовательности
,…
Ā, неубывающая по каждой из
первых n
координат. Рассмотрим n+1-вую координату в этой
последовательности. Если в последовательности
![]() ,
, ![]() ,…
ĀĀсуществует бесконечно много векторов, имеющих в качестве n+1-вой координаты
w, тогда выберем эту бесконечную подпоследовательность, которая не убывает
(постоянна) по n+1-вой координате. Если только конечное число векторов
имеют w в качестве n+1-вой
координаты, то рассмотрим бесконечную последовательность
целых, являющихся значениями n+1-вых координат.
По лемме 4.2 эта последовательность имеет бесконечную неубывающую подпоследовательность. Она определяет в
последовательности
,…
ĀĀсуществует бесконечно много векторов, имеющих в качестве n+1-вой координаты
w, тогда выберем эту бесконечную подпоследовательность, которая не убывает
(постоянна) по n+1-вой координате. Если только конечное число векторов
имеют w в качестве n+1-вой
координаты, то рассмотрим бесконечную последовательность
целых, являющихся значениями n+1-вых координат.
По лемме 4.2 эта последовательность имеет бесконечную неубывающую подпоследовательность. Она определяет в
последовательности ![]() ,
, ![]() ,…
бесконечную подпоследовательность
векторов, которые не убывают по своей n+1-вой координате.
,…
бесконечную подпоследовательность
векторов, которые не убывают по своей n+1-вой координате.
В любом случае имеется подпоследовательность векторов, неубывающая по каждой из n+1 координат. “
Докажем следующую теорему.
Теорема 4.1. Дерево достижимости сети Петри конечно. “
Доказательство. Докажем методом от противного. Допустим, что дерево достижимости бесконечно. Тогда по лемме 4.1 (и так как число вершин, следующих за каждой вершиной в дереве, ограничено числом переходов m) в нём имеется бесконечный путь x0,x1,x2,… , исходящий из корня x0. Тогда m[x0], m[x1], m[x2],… — бесконечная последовательность n-векторов. над NatÈ{w}, а по лемме 4.3 она имеет бесконечную неубывающую подпоследовательность m[xk0]£m[xk1]£m[xk2]£….. . Но по построению дерева достижимости m[xi]¹m[xj] (для i¹j), поскольку тогда одна из вершин была бы дублирующей и не имела следующих за собой вершин. Следовательно, это бесконечная строго возрастающая последовательность m[xk0]<m[xk1]<m[xk2]….. . Но по построению, так как m[xi]<m[xj] нам следовало бы заменить по крайней мере одну компоненту m[xj], не являющуюся w, на w в m[xj]. Таким образом, m[xk1] имеет по крайней мере одну компоненту, являющуюся w, m[xk2] имеет по крайней мере две w-компоненты, а m[xkn] имеет по крайней мере n w-компонент. Поскольку маркировки n-мерные, m[xkn] имеет во всех компонентах w. Но тогда m[xkn+1] не может быть больше m[xkn]. Пришли к противоречию, что доказывает теорему. “
4.2.2. Анализ свойств сетей Петри на основе дерева достижимости.
Анализ безопасности и ограниченности.
Утверждение 4.1. Сеть Петри ограниченна тогда и только тогда, когда символ w отсутствует в еёĀ дереве достижимости. Ž
Краткое обоснование. Присутствие символа w Āв дереве достижимости (m[х](p)=w для некоторой вершины x и позиции p) означает, что для произвольного положительного целого k существует достижимая маркировка со значением в позиции p, большим, чем k (а также бесконечность множества достижимых маркировок). Это, в свою очередь, означает неограниченность позиции p, а следовательно, и самой сети Петри.
Отсутствие символа w в дереве достижимости означает, что множество достижимых маркировок конечно. Следовательно, простым перебором можно найти верхнюю границу, как для каждой позиции в отдельности, так и общую верхнюю границу для всех позиций. Последнее означает ограниченность сети Петри. Если граница для всех позиций равна 1, то сеть Петри безопасна. •
Анализ сохранения.
Присутствие символа w в дереве достижимости сети Петри заведомо влечёт её несохранение. Рассмотрим свойство сохранения только относительно позиций, маркировка которых отлична от w для всех вершин дерева достижимости сети Петри. Так как дерево достижимости конечно, для каждой вершины-маркировки можно вычислить сумму маркировки. Если такая сумма для каждой вершины совпадает с суммой для начальной вершины-маркировки, то сеть Петри является сохраняющей. В противном случае сеть не является сохраняющей.
Анализ покрываемости.
В задаче покрываемости требуется для заданной маркировки m' определить, достижима ли маркировка m"³m'. Такая задача решается путём простого перебора вершин дерева достижимости. При этом ищется такая вершина х, что m[x]³m'. Если такой вершины не существует, то маркировка m' не является покрываемой. Если она найдена, то m[x] определяет покрывающую маркировку для m' Если компонента маркировкиĀ m[x], соответствующая некоторой позиции p совпадает с w, то конкретное её значение может быть вычислено. В этом случае на пути от начальной маркировки к покрывающей маркировке m[x] имеется последовательность запусков переходов, которая может неограниченно повторяться и неограниченно увеличивать значение маркировки в позиции p. Число этих повторений должно быть таким, чтобы значение маркировки в позиции p превзошло или сравнялось с m'(p).
Анализ потенциальной живости.
Утверждение 4.2. Переход t сети Петри является потенциально живым, тогда и только тогда, когда он метит некоторую дугу в дереве достижимости этой сети. •
Доказательство очевидно.
Ограниченность метода дерева достижимости. Как видно из предыдущего, дерево достижимости можно использовать для решения задач безопасности, ограниченности, сохранения и покрываемости. К сожалению, в общем случае его нельзя использовать для решения задач достижимости и активности, эквивалентности, а также для определения возможной последовательности запусков. Решение этих задач ограничено существованием символа w. Символ w означает потерю информации: конкретные количества фишек отбрасываются, учитывается только существование их большого числа.
4.2.3. Матричные уравнения.
Второй подход к анализу сетей Петри основан на матричном представлении сетей Петри. Альтернативным по отношению к определению сети Петри N в виде (P,T,I,O) является определение сети N в виде двух матриц D- и D+, представляющих входную и выходную функции I и .O. Пусть каждая из матриц D- и D+ имеет m=êTê строк (по одной на переход) и n=êPê столбцов (по одному на позицию).
Определение 4.8. Матричный вид сети Петри N=(P,T,I,O) задаётся парой (D-,D+), где
Ę D-[k,i]=^#(pi,tk) – кратность дуги, ведущей из позиции pi в переход tk.
Ę D+[k,i]=#^(tk,pi) – кратность дуги, ведущей из перехода tk в позицию pi,
для произвольных 1£k£m, 1£i£n. ‡
ĀĀĀĀĀĀĀĀĀ Пример 4.3. Матричное представление сети Петри из примера 4.2.
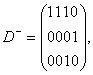 ĀĀ
ĀĀ
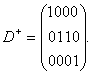
ĀĀĀĀĀĀĀĀĀ Ž
Пусть e[k] — m-вектор, k-тый элемент которого равен 1, а остальные равны 0. Переход tk, 1£k£m, в маркировке m разрешен, если m³e[k]×D-. Результатом запуска разрешённого перехода tk в маркировке m является следующая ниже маркировка m’:
m’=m - e[k]×D- + e[k]×D+==m + e[k]×D,
где D=(D+ - D-) — составная матрица изменений.
Результатом запусков последовательности переходов s=tk1,tk2,…,tkr в маркировке m является следующая ниже маркировка m’:
m’=m + e[k1]×D + e[k2]×D +…+ e[kr]×D==m + f(s)×D,
где f(s)=(e[k1] + e[k2] +…+ e[kr]) – вектор запусков последовательности переходов tk1,tk2,…,tkr. При этом i-тый элемент (где 1£i£m) вектора f(s) — это число запусков перехода ti в такой последовательности. Вектор запусков, следовательно, является вектором с неотрицательными целыми элементами.
Для демонстрации полезности
такого матричного подхода к сетям Петри рассмотрим, например, задачу
сохранения. Пусть вектор взвешивания ![]() Ā— это вектор-столбец с n=êPê элементами;
m — начальная маркировка; а
m' — произвольная достижимая
маркировка. Для выполнения сохранения необходимо, чтобы выполнялось равенство
Ā— это вектор-столбец с n=êPê элементами;
m — начальная маркировка; а
m' — произвольная достижимая
маркировка. Для выполнения сохранения необходимо, чтобы выполнялось равенство
m×![]() =m'×
=m'×![]() .
.
Теперь, поскольку m' достижима, существует последовательность запусков переходов
s, которая переводит сеть из
m в m'. Поэтому
m’=m + f(s)×D. Следовательно, m×![]() =m'×
=m'×![]() =(m+ f(s)×D)×
=(m+ f(s)×D)×![]() =m×
=m×![]() + f(s)×D×
+ f(s)×D×![]() ,
поэтому f(s)×D×
,
поэтому f(s)×D×![]() =0. Поскольку это должно быть
верно для всех f(s) (так как
m' — произвольная достижимая маркировка), имеем
D×
=0. Поскольку это должно быть
верно для всех f(s) (так как
m' — произвольная достижимая маркировка), имеем
D×![]() =0.
=0.
Таким образом, справедливо следующее замечание:
Замечание 4.5. Сеть Петри является сохраняющей
тогда и только тогда, когда существует такой неотрицательный, ненулевой вектор
![]() , что D×
, что D×![]() =0. Это обеспечивает простой алгоритм проверки
сохранения, а также позволяет получать вектор взвешивания
=0. Это обеспечивает простой алгоритм проверки
сохранения, а также позволяет получать вектор взвешивания ![]() .
.
Матричный подход также может быть применён для исследования достижимости. Предположим, что маркировка m' достижима из начальной маркировки m. Тогда существует последовательность (возможно, пустая) запусков переходов s, которая приводит из m в m'. Это означает, что f(s) является неотрицательным целым решением следующего матричного уравнения для х – m'=m + x×D.
Замечание 4.6. Если m' достижима из m, тогда уравнение m'=m + x×D имеет решение в неотрицательных целых числах; если это уравнение не имеет решения, тогда m' недостижима из m.
Основные недостатки такого матричного подхода к анализу достижимости состоят в следующем: Условие достижимости из замечания 4.6 является необходимым, но не достаточным. Поэтому вектору-решению уравнения m'=m+x×D может не соответствовать допустимой последовательности запусков переходов. Вектор-решение содержит информацию о числе запусков переходов, но не содержит информации о порядке их запусков. ПоэтомуĀ возникает проблема построения по вектору-решению допустимой последовательности запусков переходов.